Prediction is the wrong word to use. Nevertheless, I use it myself also as the correct word – prevision – is not yet known enough. The problem with prediction is that prediction suggests that one knows the future with absolute certainty. Whereas in reality you only see a future that is a possibility and has a probability. So the word “Prevision” perfectly captures that sense. You have a vision of the future before it actually happens. That is the reason why professor De Finetti introduced the word “prevision” and why he wants us to stop using the word “prediction” and replace it with the word “prevision”.
As I give a lot of predictions, or better yet previsions, of football matches on my Twitter account, I am often confronted with people who tell me to my face that my prediction was wrong. And sometimes they are right. Fans don’t like negative predictions for their team and love the analyst to be wrong. And in those cases I am happy to be wrong. In fact, when we use these predictions to help clubs prepare for matches, then we are actually working to make sure that the prediction turns out wrong.
So let’s look at a recent prediction that was wrong:

The end result was a 3-1 win for VVV. That is a three goal difference with our prediction, in the sense that RKC had to score three more goals for the prediction to become true. So the first reason why this prediction is wrong, is that it is not a case of happenstance. It would have been very likely to be happenstance if the goal difference to make the prediction true would have been one.
If we dive into the underlying FBM model RKC has a 42% chance to win, VVV a 28% chance to win and there was a 30% chance for a draw. Nate Silver of 538 uses these probabilities to argue that he is never wrong.
If you want to make us look bad, you’ll have a lot of opportunities to do so because some — many, actually — of these forecasts will inevitably be “wrong.” – Nate Silver
If we were to follow Nate Silver’s argument then we would say that even though we gave VVV only a 28% chance, 28% chance still happen, so we were right after all! We would then continue to use all kinds of mathematics to show that a large number of predictions on average pretty much follow reality. Of course, we have done so. And for the first 144 matches, our prediction error was little more than 1% whereas the sports betting industry had a prediction error of 4%. We could then use Brier’s Score to further proof how well our predictions match up with reality. But although this is completely mathematical sound to do, it is not what I want to do.
Previsions can be wrong
The reason why I think we have to move beyond a mere mathematical check on whether a prediction was right, has to do with using previsions instead of predictions. If you also take a prevision only to be a mathematical number, then it doesn’t matter. But if you take prevision literally, i.e. as a vision of the future before the future happens, then it is not only possible to see that a prevision is wrong even though I gave the winning team a 28% chance of winning, a prevision can even be wrong even though it did give the winning team the biggest chance of winning. For the favorite might have won in a completely different fashion than that the prevision foretold. Especially in all cases where the favorite only wins with one goal difference, there is a decent chance that this was happenstance and if so it might invalidate the prevision even if the prevision was right.
If you can be wrong even when you are right, the opposite is also possible. In that case you are right even if you are wrong. Here is an example:
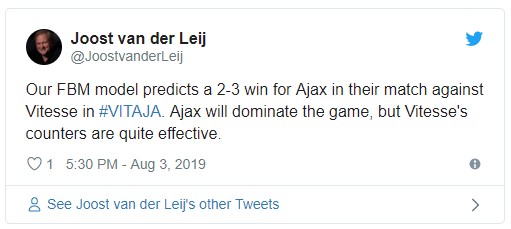
The end result was a 2-2 draw. Our FBM model gave Ajax a 53% chance to win, Vitesse a 35% chance and there was only a 12% chance of a draw. Nevertheless, it was a draw. Yet, the prevision was correct. Ajax did dominate the game and Vitesse’s counts were very effective. As it was only a one goal difference for a different outcome, this is a case of happenstance. In fact, Ajax shot a ball on the post and had quite a few other chances.
The reason why our model had this prevision is because the model bases it chances on three values: the percentage of domination, the percentage of chances and the relative attack power of each team. In this example Ajax had a domination of 84% versus Vitesse that had a domination of 8%. Ajax had 66% of the chances versus Vitesse 34%. And the Ajax had an attack power of 2.6 (rounded this gives the 3 goals for Ajax in the prevision) versus Vitesse of 1.9 (rounded this gives the 2 goals for Vitesse).
The combination of a high domination for Ajax with still a lot of attack power for Vitesse, gives the prevision of a match where one team dominates (Ajax), but where the other team counters effectively (Vitesse).
Mathematically, this prevision was quite inaccurate. As a literal prevision, it was quite accurate.
Mathematics versus a literal prevision
In my view, for a football club, a literal prevision, in the sense of describing qualitatively how the match will unfold, is more valuable than a quantitative description in terms of probability. The reason is that if a manager doesn’t like the literal prevision, he can take measures to prevent the unwanted prevision from ever happening.
When you read our match preparation of the match between PSV and Basel, you see that we lower our initial estimation of the chance of PSV winning once we get the actual lineup. The original prevision was based upon the lineup in the previous match. As soon as the actual lineups for the match are known we update our model and get an updated prevision. Originally, we foresaw a high chance of PSV winning. In our updated prevision we saw a much lower chance of PSV winning. In the end PSV won the match 3-2.
Mathematically, that means that our original prevision was much more accurate than our updated prevision. Nevertheless, for those who have watched the match, almost everyone would agree that the updated prevision – the one with a much lower chance of PSV winning – was more accurate. Until 5 minutes before the end of the match, PSV was down 1-2. PSV was very lucky to score twice in the dying moments of the match. Again, because only a one goal difference would have meant a different outcome, this is a case of happenstance. Yet, the manager would have found the less accurate updated prevision a lot more helpful than the mathematically more accurate original prevision.
Here you have an excellent example of why football clubs should never only use data. Instead they need to always use experts that can look beyond the numbers. Being mathematically correct does not mean that your numbers are actually useful. They might in fact be quite misleading. And the other way around: a prevision that actually helps the team increase the chance of winning, doesn’t have to be mathematically the best prevision.
